Masse
S. Burghardt (05.2019) MINTwiki.de/Masse
| Physikalische Größe | |
|---|---|
| Name | Masse |
| Formelzeichen | |
| SI-Einheit | Kilogramm |
| Einheitenzeichen | Basiseinheit |
Die Masse (engl. mass) ist eine grundlegende Eigenschaft von Materie und wird in der Einheit kg (Kilogramm) gemessen.
Diese Einheit wird seit 2019 über die Festlegung der Planckschen Konstanten durch die bereits neu definierten Einheiten von m (Meter) und s (Sekunde) definiert.
Die Masse entfaltet zweierlei physikalische Wirkungen, Trägheit und Gravitation. Dementsprechend unterscheidet man träge und schwere Masse, die nach dem Äquivalenzprinzip gleichzusetzen sind.
Ferner sollte man die Masse von Begriff Gewicht abgrenzen. Auf der Erde nimmt man i.d.R. eine konstante Gravitation an, wodurch die Masse näherungsweise proportional zur Gewichtskraft ist. Daraus folgt dann, dass man die Masse hier z.B. mit einer Federwaage bestimmen kann. Somit wäre der Begriff des Gewichts vom äußeren Gravitationsfeld abhängig. Die Masse ist es nicht.
| Plancksche Konstante |
Inhaltsverzeichnis
Eigenschaften und Beziehungen zu anderen Größen
| Kraft | |
| Impuls | |
| Geschwindigkeit | |
| Lichtgeschwindigkeit | |
| Energie | |
| Lorentzfaktor |
Impulserhaltung
Der Impuls ist als eine der Geschwindigkeit proportionale Erhaltungsgröße definiert. Aus dieser Definition kann man die Masse als Größe herleiten und es zeigt sich der Unterschied zwischen klassischer und relativistischer Betrachtung. Man schreibt hier dem Impuls zunächst allgemein als ein Produkt der Geschwindigkeit mit einem ggf. geschwindigkeitsabhängigen Faktor:
Betrachtet man nun einen zentrischen inelastischen Stoß zweier gleicher Körper mit genau entgegengesetzten Geschwindigkeiten, dann addiert man die Geschwindigkeiten zu einem dazu bewegten Beobachter. Erfolgt dies mittels Galilei-Transformation, dann folgt daraus eine Massendefinition als eine vom Inertialsystem unabhängige, additive Erhaltungsgröße:
Geht man bei der Transformation auf den Beobachter von der Lorentz-Transformation aus, dann ergibt sich:
Hierin sind die Ruhemassen der Körper und man kann eine geschwindigkeitsabhängige "relativistische Masse" als rechnerische Hilfsgröße definieren:
Hier stellt man sich vor, dass die Masse und damit die Trägheit eines Körpers mit steigender Geschwindigkeit zunimmt. Das ist so nicht korrekt kann auch nicht für die Charakterisierung der Trägheit so einfach verwendet werden. Die Definition der Masse ist einzig an die Ruhemasse, , gekoppelt.
Invarianz gegenüber Bezugssystemen
Die Masse wird sowohl von der klassischen Physik als auch unter Berücksichtigung relativistischer Theorie als Invariante betrachtet. Ein Körper hat also in jedem Bezugssystem die gleiche Masse, die sich durch Transformation (Galilei- respektive Lorentz-Transformation) nicht ändert.
Additivität und Äquivalenz von Masse und Energie
In der klassischen Physik ist die Summe der Massen zweier Körper gleich der Masse eines aus diesem Massen zusammengefügten Körpers (siehe Impuls). Der innere Energiezustand der Massen wird dabei nicht berücksichtigt, da dieser in der klassischen Betrachtung mit der Masse nichts zu tun hat. Die kinetische Energie berechnet sich dementsprechend:
Diese Definition würde beliebig große Geschwindigkeiten erlauben, die es aber gemäß der speziellen Relativitätstheorie nicht gibt. Hier ist die Äquivalenz von Masse und Ruheenergie, , ein Naturgesetz:
Dabei ist die Lichtgeschwindigkeit, , eine Naturkonstante und die obenstehende Gleichung ist zugleich die moderne Defininitionsgleichung der Masse bzw. Ruhemasse. Demgemäß ist die kinetische Energie die Differenz aus der Gesamtenergie eines Körpers und dessen Ruheenergie:
Trägheit
Nach dem ersten Newtonschen Axiom verbleibt ein Körper in Ruhe oder gleichförmiger Bewegung, sofern er nicht durch einwirkende Kräfte zur Änderung seines Zustands gezwungen wird. In dieser Beziehung ist die Trägeheit des Körpers ein Maß des Widerstands eines Körpers gegen die Änderung seines Bewegungszustandes. In der klassichen Mechanik ist die Geschwindigkeitsänderung (Beschleunigung) von der Ausgangsgeschwindigkeit unabhängig:
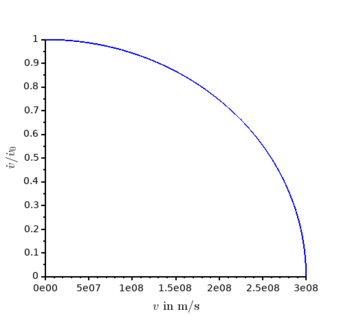
Damit würde sich ein Körper theoretisch bis zu einer unendlichen Geschwindigkeit beschleunigen lassen. Da die Lichtgeschwindigkeit aber die höchste theoretische Geschwindigkeit ist, ist das nicht möglich. Hier leitet man die Gleichung aus dem Impuls ab:
Für wird also die Trägheit unendlich, was letztlich die Beschleunigung begrenzt (Abb. 1). Für ist der Fehler von Newtons Gleichung vernachlässigbar, weshalb sie in den meisten technischen Anwendungen verwendet wird. Ein Fehler von 1 ‰ wird erst bei über 13 Mio m/s überschritten.
Gravitation
In der klassixchen Mechanik wird die Gravitation als eine gegenseitige Anziehungskraft von zwei Massen beschrieben, die in Richtung der sie verbindenden Schwerpunktachse wirkt:
Hier ist eine Naturkonstante und der Abstand der beiden Massenschwarpunkte. Man kann also aus jeder Masse ein Kraftfeld ableiten, das man Gravitationsfeld nennt und damit eine räumlich verteilte Gravitationsbeschleunigung begründet - auf der Erde entspricht diese der Fallbeschleunigung, .
Dichte, Volumen und Massenmodelle
Die Dichte (oder besser Massendichte) ist ein Begriff aus der Kontinuumstheorie und damit ein Potentialfeld im Raum. Für ein abgeschlossenes Volumen, , ergibt sich die Masse:
Im physikalischen Sinn kann jeder Masse ein Volumen zugeordnet werden. Gerade in der Ingenieurwissenschaft kann es allerdings zweckmäßig sein, die Masse als Flächen- oder Liniendichte zu definieren, die als Modell für eine dünne Platte resp. einen Balken dient. Für dynamische Berechnungen verwendet man häufig das Modell einer Punktmasse im Schwerpunkt eines starren Körpers.
Messung
Da man auf der Erde ein näherungsweise homgenes Gravitationsfeld vorfindet, kann die Masse eines makroskopischen Körpers durch Messung der Gewichtskraft mittels einer Waage bestimmt werden. Hier kann man eine direkte und indirekte Wägung unterscheiden. Bei der Balkenwaage kann man eine Masse direkt mit einer Referenzmasse vergleichen, wobei man sich das Hebelgesetz zunutze macht:
Bei der indirekten, heute bei weitem dominierenden Methode, das ist die Waage ein Kraftmesser, der mittels Referenzmassen kalibriert wird.