Einmassenschwinger
S. Burghardt (11.2018) MINTwiki.de/Einmassenschwinger
| Lage des Massepunkts | |
| Weganregung am Fußpunkt | |
| Kraftanregung an der Masse | |
| Punktmasse | |
| Federkonstante | |
| Dämpfungsfaktor |
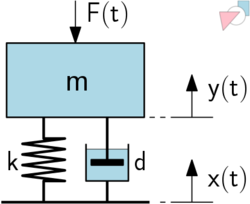
Ein Einmassenschwinger (engl. single degree of freedom system -> SDOF) repräsentiert das einfachste mathematische Modell eines eindimensionalen schwingungsfähigen mechanischen Systems mit einem Bewegungsfreiheitsgrad. Er besteht aus einer invarianten Masse , einer linearen Feder mit der Steifigkeit und ggf. einem proportionalen Dämpfer mit dem Dämpfungsfaktor . Wird nun die dynamische Last (Erregung) betrachtet, die auf die Masse wirkt, dann ergibt sich durch Einsetzen einer d'Alembertschen Trägheitslast aus dem Kräftegleichgewicht die Bewegungsdifferentialgleichung:
Die Vorzeichen orientieren sich hier an Abb.1 und können auch anders definiert werden. Für eine freie Schwingung kann diese Gleichung mit dem Ansatz im Zeitbereich gelöst werden.
Die große technische Bedeutung für das Modell des Einmassenschwingers ergibt sich aus der Tatsache, dass alle Feststoffe, sofern man deren Schwingungsfähigkeit betrachtet, in Prinzip verknüpfte Systeme aus Masse, Steifigkeit und Dämpfung sind. Das Verständnis des Einmassenschwingers ist damit die Grundlage für die Beschreibung komplexerer Systeme mit einer Modalanalyse.
Inhaltsverzeichnis
Übertragungsfunktionen und Frequenzgang
Durch Laplacetransformation können LZI-Übertragungsfunktionen aufgestellt werden. Es ergibt sich für die Krafterregung bzw. Wegerregung:
Diese Übertragungsfunktionen können genutzt werden, um die transiente Bewegungsgleichung als Anfangswertproblem mit beliebigen Eingangsfunktionen numerisch zu simulieren. Das passive System des Einmassenschwingers ist dementsprechend ein Verzögerungsglied zweiter Ordnung (PT2-Glied).
Eine analytische Lösung kann man für einige spezielle Anregungsfunktionen ermitteln.
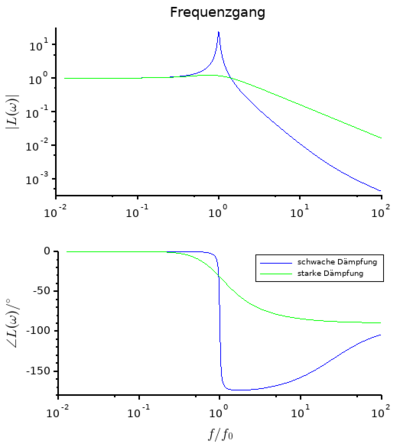
Für kann man mit der Übertragungsfunktion den komplexen Frequenzgang aufstellen, um Verstärkung und Phasenverschiebung einer harmonischen Anregung zu ermitteln. Besonders anschaulich lässt sich das für die Weganregung darstellen, was in Abb. 2 dargestellt ist.
Man erkennt hier, dass die Amplitude für kleine Frequenzen der Anregungsamplitude entspricht und der Einmassenschwinger gleichphasig der Anregung folgt. Das gilt bis zu einer Grenzfrequenz, bei der je nach Dämpfung eine Amplitudenverstärkung auftreten kann (ohne Dämpfung wird diese unendlich). Ab der Grenzfrequenz wird die Anregung nur noch abgeschwächt übertragen und die Masse schwingt gegenphasig.
Resonanzfrequenz und charakteristische Parameter
| Eigenkreisfrequenz | |
| Abklingkonstante | |
| Dämpfungsgrad | |
| logarithmisches Dekrement |
Nun hat jeder Einmassenschwinger eine Resonanzfrequenz, , bei der die Amplitudenverstärkung maximal wird. Diese muss sich aus den Polstellen der Übertragungsfunktion ergeben. Dazu deklariert man häufig die Abklingkonstante und die Eigenkreisfrequenz :
Die Lösung ist:
Man sieht hier, dass die Eigenfrequenz komplexe Werte annimmt, sofern eine Dämpfung existiert. Ein entscheidendes Kriterium des Systemverhaltens ist dementsprechend der Term unter der Wurzel. Für diesem gibt es auch das Lehrsche Dämpfungsmaß, das eine modale Dämpfung beschreibt.
Impulsantwort
| Impuls | |
Ist die Kraftfunktion ein Diracimpuls, , in technischer Hinsicht also z.B. ein Schlag mit einem Impulshammer, dann ergibt sich aus der Übertragungsfunktion die Bewegungsfunktion zunächst im Frequenzbereich:
Zur Rücktransformation braucht es eine Partialbruchzerlegung
Damit ergibt sich durch Laplace-Rücktransformation (Korrespondenztabelle) die transiente Funktion:
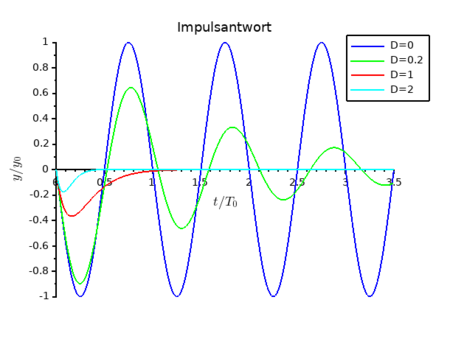
Das Aussehen der Funktion hängt von der Dämpfung ab. Für schwingungsfähige Systeme wird real, und man kann die Exponentialterme mit der Eulerformel auflösen. Für den aperiodischen Grenzfall wird und man muss die transiente Funktion mit dieser Prämisse neu herleiten. Die folgende Tabelle zeigt die Funktionen für verschiedene Dämpfungsbereiche, die in Abb. 3 dargestellt sind.
| instabiles System | ||
| ungedämpfte Schwingung | ||
| gedämpfte Schwingung | ||
| aperiodischer Grenzfall | ||
| Kriechfall |
Sprungantwort
| Sprungfunktion | |
Eine freie Schwingung kann man durch eine Sprungfunktion der Weganregung modellieren.
Die Partialbruchzerlegung kann man von weiter oben übernehmen. Die Terme können auch als Produkt mit aufgelöst werden:
Die direkte Anwendung der Korrespondenztabelle ergibt zunächst die Zeitfunkion als komplexe Summe:
Das kann man durch Differenzieren und Vereinfachen weiter auflösen, was eine für ... eine harmonische Funktion ergibt: